R の形態測定学パッケージ〈shapes〉:「いろは」の「い」
三中信宏
Copyright (c) 2006-2008 by MINAKA Nobuhiro. All rights reserved.
〈R〉のパッケージ〈shapes〉(2007年10月29日に最新版 version 1.1-0 が公開されました)は,幾何学的形態測定学(geometric morphometrics)の手法を〈R〉を用いて計算するプログラムです.〈shapes〉を用いることにより,比較すべき形態上に設定された標識点(landmark)の2次元または3次元の座標データから,重心サイズの計算・プロクラステス整列・ブックステイン形状座標・ケンドール形状空間上のリーマン計量など,幾何学的形態測定学による形状比較をするためのさまざまな数値が計算できるだけでなく,それらを図示することもできます.さらに,形状集団の間の平均形状に関する差の検定を多変量分散分析(MANOVA)とリサンプリングによって実行することもできます.
〈shapes〉の詳細についての情報は,開発者である Ian Dryden 博士の下記サイト:
The Shapes Package : Statistical Shape Analysis in R
を参照してください.このサイトには〈shapes〉を使う上で役に立つマニュアル(pdf)ならびにチュートリアル(txt)が置かれています.もちろん,〈R〉内のヘルプを参照することもできます.
本来ならば,著者自身の手になるこれらのドキュメントを見れば,それ以上の補足説明をするのは蛇足以外のなにものでもありません.しかし,私が試用しているうちに,そもそも自分のデータを〈shapes〉の形式に合わせて入力するところにやや高いハードルがあるように感じました.そこで,自分のデータを出発点として,データのハンドリングから出発して一連の形態測定学的解析を〈shapes〉で行なう手順を備忘メモとしてまとめておくことにしました.
なお,この〈shapes〉は下記の著書の内容を踏まえて書かれたプログラムです:
Ian Dryden and Kanti V. Mardia『Statistical Shape Analysis』(1998年刊行,John Wiley & Sons,ISBN:0-471-95816-6→目次)
したがって,幾何学的形態測定学に関する基本的な理論と概念については本書を参照してください.あるいは,私がつくっている別の講義用サイト〈幾何学的形態測定学:「かたち」の数学と統計学〉と〈自然人類学における幾何学的形態測定学の諸手法〉,そして〈形態測定学に関する教科書および参考書リスト〉も参考になるでしょう.
1. データ・ファイルをつくる
標識点の個数を k とし,その次元を m とします.たとえば,2次元座標の標識点の組み(xi, yi)(i = 1, 2, ……, k)からなるデータがあるとき:
x1 y1 x2 y2 …… xk yk
の書式に従ってテキストファイルの1行に書けば(セパレータはスペース),それでデータ・ファイルは完成です.さらに,続く形状の座標データがあるときは,改行した上で,新しい行に同じ書式でデータを書けば複数個の形状についての座標データを一つのテキストファイルとして用意することができます.
いま,次の二つのデータ・ファイルを用意します:
BeforeForm.dat
-1.0 0.0 1.0 0.0 0.0 1.0 0.0 -1.0
AfterForm.dat
-1.0 0.0 1.0 0.0 0.0 1.0 0.0 -1.0
この二つは変形前と変形後の形状を表すものと理解してください.
2. データ・ファイルをRに読込む
R を起動して,〈shapes〉を呼び出します.(〈shapes〉パッケージはすでにインストールされているものとします.また,指定された作業ディレクトリにデータ・ファイルが置かれているとします):
> library(shapes)
読込むデータ・ファイルの標識点数 k と次元数 m を指定します:
> k <- 4 #ランドマーク数 > m <- 2 #次元数外部データ・ファイルを読込むときは「read.in()」を使用します:
> before <-read.in("BeforeForm.dat",k,m) #変形前形状データ読込み
> after <-read.in("AfterForm.dat",k,m) #変形後形状データ読込み
このとき,読込まれたデータは次のような構造になっています:
> before
, , 1
[,1] [,2]
[1,] -1 0
[2,] 1 0
[3,] 0 1
[4,] 0 -1
> after
, , 1
[,1] [,2]
[1,] -0.5 0
[2,] 2.0 0
[3,] 0.0 1
[4,] 0.0 -1
「read.in()」で読込まれた n 標本データは,Rの中では「k×m×n」という3次元マトリクスに構造化されます.したがって,第j番目(j=1,2,……, n)の標本のデータだけを切り出すためには「[, , j]」と指定すればいいわけです.上の例では,n=1 ですから:
> before[, , 1] [,1] [,2] [1,] -1 0 [2,] 1 0 [3,] 0 1 [4,] 0 -1 > after[, , 1] [,1] [,2] [1,] -0.5 0 [2,] 2.0 0 [3,] 0.0 1 [4,] 0.0 -1
となります.
3. 形状を描画する
上記の手順で読込んだデータをそのまま描画するには「plotshapes()」という関数を使います:
> par(mfrow=c(1,2)) #グラフ描画スタイルの指定 > plotshapes(before, after) #変形前(下図左)と変形後(下図右)
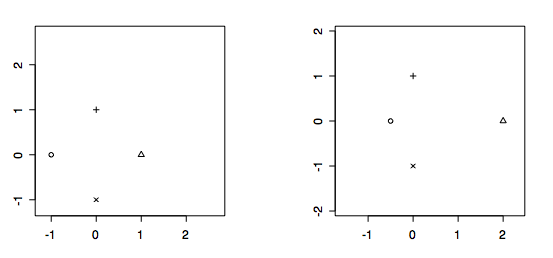
複数標本を含むテストデータとして,まずはじめに〈shapes〉にもともと含まれているゴリラ頭骨のデータ(二次元座標データ)を使いましょう.♂データは「gorm.dat」(29標本),♀データは「gorf.dat」(30標本)と指定できます.複数標本データの場合,ファイル名で描画すると全標本を描きますが,標本番号を指定するとそれだけが描かれます:
> data(gorf.dat) #データ呼び出し > data(gorm.dat) #データ呼び出し > plotshapes(gorm.dat) #ファイル中の全標本の描画[下図] > plotshapes(gorm.dat[,,8]) #第8標本のみ描画 > plotshapes(gorm.dat[,,3:9]) #第3〜9標本を描画
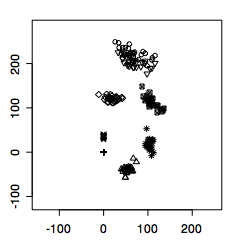
次に,三次元の標識点データの例として,これも〈shapes〉に入っているマカクの♂頭骨データ「macm.dat」(9標本)を使います.三次元データの場合は,通常の二次元表示の関数「plotshapes()」に加えて,三次元表示のための別関数「shapes3d()」を使うことができます:
> data(macm.dat) #データ呼び出し > plotshapes(macm.dat) #ファイル中の全標本の二次元描画[下図左] > shapes3d(macm.dat, loop=0) #同三次元描画[下図右]
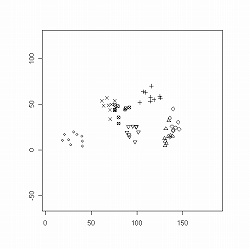

関数「shapes3d()」による散布図(左図)は,マウスなどを用いて三次元空間の中で自由に回転させることができます.
4. 形状集団のプロクラステス整列
複数標本に関する一般化プロクラステス分析(GPA)は関数「procGPA()」を用いて行ないます(2標本間では通常のプロクラステス分析 OPA が使用できます:procOPA()):
> gorm <- procGPA(gorm.dat) #gorm.datのGPA > gorf <- procGPA(gorf.dat) #gorm.datのGPA
procGPA() から出力されるのは,重心サイズ($size)・整列後の座標($rotated)・主成分(pcar)・形状間のリーマン距離($rho)・平均形状($mshape)などです(詳細は「> help(procGPA)」を参照).たとえばプロクラステス整列された標本とその平均形状を描画するには,出力の中の該当項目プロットすればよいということです:
> plotshapes(gorm$rotated) #プロクラステス整列された全標本の描画[下図左] > plotshapes(gorm$mshape) #全整列標本の平均形状の描画[下図右]
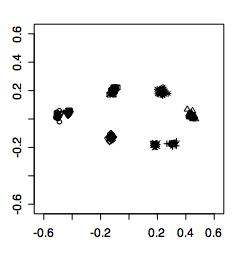
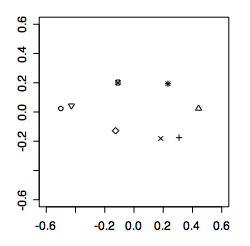
三次元の場合も同様です:
> macm <- procGPA(macm.dat) #macm.datのGPA > shapes3d(macm$rotated) #プロクラステス配列[下図左] > shapes3d(macm$rotated, loop=0) #平均形状[下図右]


これらの三次元散布図もまた空間内で自由に回転させることができます.
5. GPAに伴う主成分分析と作図
> procGPA()を用いてプロクラステス整列された形状の標識点組のばらつきを主成分分析(shapepca())を用いて要約します.ただし,ここでの主成分分析は整列座標データの分散共分散行列に対する固有値分解であって,相対歪み解析のように平均形状からの仮想変形伴うスプライン関数の係数に関する分散共分散行列の特異値分解ではありません.
デフォルト(type = "r")では,主成分軸に沿って−3 s.d.〜+3 s.d.(s.d.=標準偏差)で変化させたときの形状変化が表示されます:
> shapepca(gorm, pcno=c(1)) #デフォルト表示(第1主成分のみ)[下図]
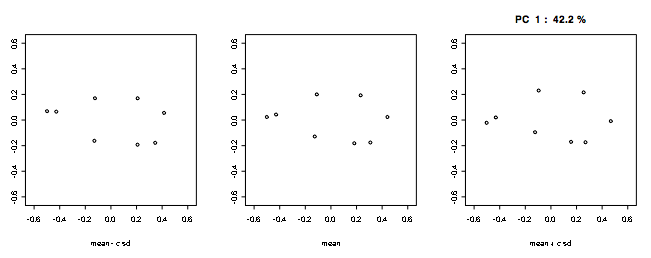
出力の表示方法は他にもあり,平均形状から+3 s.d.方向への変形をベクトル表示をしたり(type = "v"),−3 s.d.〜+3 s.d. の範囲での変形を動画表示する(type = "m")という選択肢がある:
> shapepca(gorm, pcno=c(1:2), type="v", mag=3) #ベクトル表示(第1〜2主成分,変動増幅率=3倍)[下図] > shapepca(gorm, pcno=c(1:5), type="m") #動画表示(第1〜5主成分)
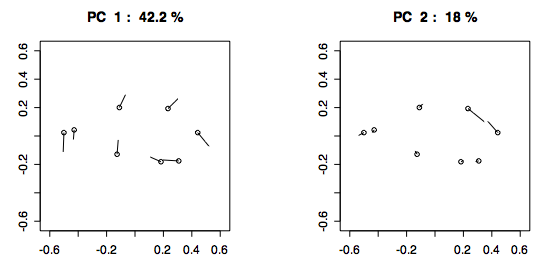
とくに,主成分軸に沿っての変動の動画表示は,形態的変異の“視覚化”のツールとしてたいへん効果的です.
三次元については,前節で用いた macm.dat のGPA出力オブジェクト「macm」をそのまま利用します.関数「shapepca()」の出力はデフォルトで三次元表示になり,各主成分軸に沿った変動は有向線分で表示できます:
> shapepca(macm, pcno=c(1:3), mag=3) #第1〜3主成分のベクトル表示.変動増幅率=3倍.
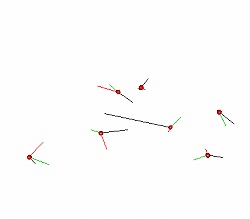
さらに,各主成分に関する座標空間内での三次元表示「shapepca3d()」を使うことができます:
> shapepca3d(macm, pcno=1)) #第1主成分の三次元表示(アニメーション付き).
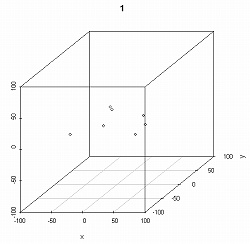
この「shapepca3d()」では,アニメーションによって座標空間内での主成分軸に沿っての変動を表示します.
6. ケンドール形状間のリーマン計量ρの計算
ケンドール形状空間上での形状差($rho)は,個々の標本と平均形状との距離ρとして > procGPA から出力されます:
> gorm$rho #gorm.dat の各標本と平均形状とのリーマン計量ρ(測地線距離) [1] 0.04798497 0.03254402 0.05051745 0.04185981 0.02686846 [6] 0.03859092 0.02947735 0.04001411 0.06006434 0.03373014 [11] 0.04445558 0.03790608 0.04346251 0.04348644 0.03451539 [16] 0.04163568 0.04529528 0.07352642 0.08154610 0.06240846 [21] 0.05104625 0.03277207 0.02999994 0.03687930 0.05800760 [26] 0.07311486 0.02945698 0.08545492 0.06615009
なお,任意の形状間のリーマン計量は「riemdist()」によって計算できます:
> riemdist(gorm$mshape, gorf$mshape) #gormとgorfの平均形状間の距離 [1] 0.05866407 > riemdist(before[,,1], after[,,1]) #4標識点からなる形状(before / after)間の距離 [1] 0.3378896
なお,外部データファイルから read.in() で読込んだ場合,標本番号で切り出してから riemdist() で計算しなければなりません.「riemdist(before, after)」ではエラーになります.
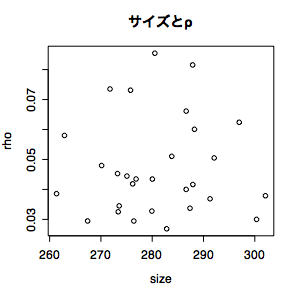
最後に,重心サイズとリーマン計量ρとの関係を図示する.
> par(mfrow=c(1,1))
> plot(gorm$size, gorm$rho, xlab = "size", ylab = "rho") #下図参照
> title("サイズとρ") #グラフへのタイトル記入
7. 形状変形のスプライン補間と作図
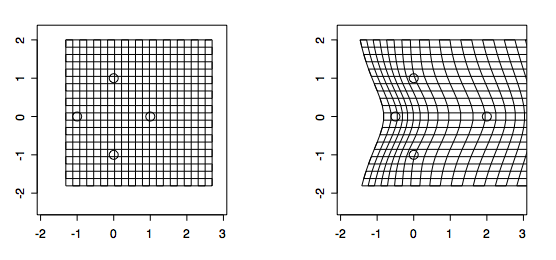
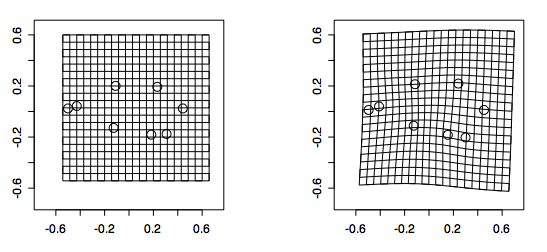
薄板スプライン関数を用いた局所的形態変形の記述は,関数「tpsgrid()」を用いて実行できます:
> par(mfrow=c(1,2)) #グラフの描画様式の指定 > tpsgrid(before[,,1], after[,,1], -1.5, -2.0, 4.0) #before→after の仮想変形[下図上] > tpsgrid(gorm$mshape, gorf$mshape, -0.6, -0.6, 1.2) #gormとgorfの平均形状間の仮想変形[下図下]
8. 集団間の形状差の検定
集団間の差異の有意性について,〈shapes〉はふたつの検定法を用意しています.ひとつは,標識点座標に関する多変量分散分析(MANOVA)を用いた平均形状の有意差検定(testmeanshapes())です:
> test1 <- testmeanshapes(gorm.dat, gorf.dat) #gormとgorfの形状差に関するMANOVA(Hotelling T2検定) Hotelling's T^2 test: Test statistic = 26.47 p-value = 0 Degrees of freedom = 12 46 > test2 <- testmeanshapes(gorm.dat, gorf.dat, Hotelling=F) #同MANOVA(Goodall F 検定) Goodall's F test: Test statistic = 22.29 p-value = 0 Degrees of freedom = 12 684
もうひとつの検定法はデータからの無作為再抽出(ブーツストラップ・リサンプリング)によるもので,いくつかの検定統計量の帰無分布における tail probability をリサンプリングによって計算します:
> resampletest(gorm.dat, gorf.dat, resamples = 200) #反復回数を200回に設定してリサンプリングする Resampling...No of resamples = 200 $lambda [1] 249.1846 $lambda.pvalue [1] 0.004975124 $lambda.table.pvalue [1] 0 $H [1] 26.47042 $H.pvalue [1] 0.004975124 $H.table.pvalue [1] 1.110223e-16 $J [1] 391.8577 $J.pvalue [1] 0.004975124 $J.table.pvalue [1] 0 $G [1] 22.28571 $G.pvalue [1] 0.004975124 $G.table.pvalue [1] 0ただし,リサンプリング回数を大きく設定すると計算時間が極度に長くなるので注意が必要です.