●系統樹と Newick format（2）：ラベルの表示●

Newick format に基づく系統樹の文字列コード化についてはすでに説明した．以下では，単系統群構造（姉妹群関係）以外の情報をどのように表現するかについて解説する．

前回は〈TreeView〉という系統樹描画ツールを用いたが，今回は〈PhyloWidget〉を使いながら説明する．その理由は〈TreeView〉はNewick format でコード化された系統樹を含む Nexus 形式のツリーファイルを必要とするのに対し，〈PhyloWidget〉は直接的に Newick format を描画する機能があるからである．

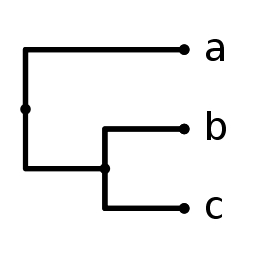
そもそも系統樹の「樹形」そのものの表示に末端点（子孫）や分岐点（祖先）の「ラベル（名前）」は必要ない．たとえば，〈PhyloWidget〉の File メニュー内の「Lord Tree」→「Manual Input」と進んで，Newick format で

　　(a , (b , c))

と入力すると，前回示したような末端の子孫すべてにラベル（a , b , c）がつく系統樹が表示される（左図）．

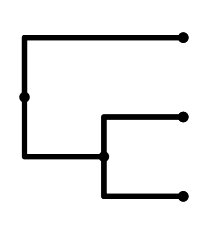
しかし，同じ入力画面でラベルのみを除去した

　　( , ( , ))

を入力すると，右図のように末端にラベルがつかない樹形のみが表示される．

●系統樹と Newick format（3）：共通祖先の表示●

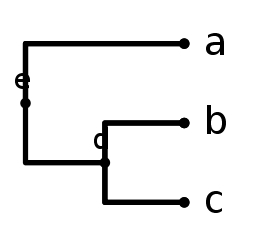
単系統群は定義によりある共通祖先の存在を前提とする．系統樹の上でそれらの共通祖先は内部分岐点に位置する．Newick format で

　　(a , (b , c) d) e

と入力すると，単系統群 (b, c) に対する共通祖先 d ならびに単系統群 (a, b, c) に対する共通祖先 e のラベルを表示できる．つまり

　　(子孫, 子孫) 共通祖先

という書式を用いれば，任意の単系統群とその共通祖先を Newick format で表示可能である（共通祖先の直前にコンマ , を入れてはいけない）．

●系統樹と Newick format（4）：枝長の表示●

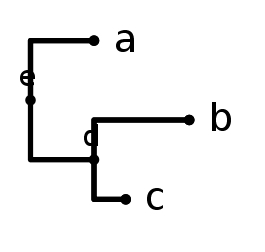
さらに，ある子孫や祖先にいたる枝の「長さ」（その定義については別の機会に述べる）を表示することもできる．いま〈PhyloWidget〉の入力画面で

　　(a:2 , (b:3 , c:1) d) e

と入力する． 「点: 数値」 という書式は「その点の直下の枝長を指定数値にする」という意味である．「View」メニューの「Branch Lengths」をオンすると，左図のように指定された枝長に比例して系統樹が描画される．

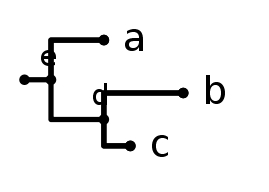
さらに，共通祖先に関しても内部枝の長さを指定することができる．

　　((a:2 , (b:3 , c:1) d:2) e:1)

上のように書くと，共通祖先 d と e の直下の枝の長さをそれぞれ「2」と「1」に指定できる．

●系統樹のタイプと描画スタイル●

上で説明したように，系統樹というグラフは，単系統群・共通祖先・ラベル・枝長などいくつかの情報を伝達する図形言語である．最近の数理系統学ではグラフ理論から借用したさまざまな用語が用いられることがある．とくに，ラベル付きであって枝長を表示しないタイプのものを「分岐図（cladogram）」，相対的な枝長をも表示したタイプを「系統樹（phylogram）」と呼ぶことが多い．いずれにせよ，系統樹リテラシーの第一歩はある系統樹にどの情報が表示されているのかを知ることである．

さらに言えば，同じタイプの分岐図や系統樹であっても，描画スタイルはいろいろある．〈PhyloWidget〉の「View」メニューの「Layout」を見ると：

			Rectangular
			Diagonal
			Circular
			Unrooted
			

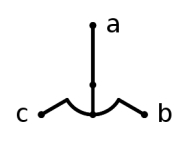
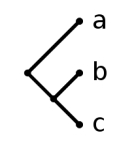
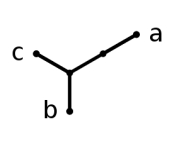
の四種類が用意されている（系統樹描画ツールによってはもっとたくさんある）．いま，上で用いた

　　(a , (b , c))

による分岐図を上の四つの形式で描画すると下記のようになる（上から下に）．描画スタイルの見かけはまったく異なるが，すべて「同一の情報」を表現していることに注意されたい．

グラフとしての系統樹については Newick format のような標準的書式がすでに過去30年の間に普及しているので，情報内容と描画方法に関しては決着がついているとみなしてよい．しかし，系統推定の方法によって系統樹を構成する概念体系（単系統群・祖先・枝長など）がすべて異なっている．次に，どのような系統推定法が現在利用されているのかについて学ぶ必要がある．

●参考文献●

• Books LLC (2010), Graph Description Languages: Dot Language, Gxl, Newick Format, Graphml, Graph Modelling Language, Xgmml, Trivial Graph Format. ISBN:9781158393213