多変量解析概論

０．はじめに：多変量空間は人間にとって生存不能である

あるデータ点が複数の変量から成るとき，われわれは「多変量データ」（multivariate data）と呼ばれるものに遭遇する．たとえば，統計言語Ｒのパッケージに含まれているデータファイルのひとつに，植物学者 Edgar Anderson が集めた Iris属の形態データがある（ファイル名：「iris」）．その一部を下記に示そう：

> data(iris)
> attach(iris)
> iris

Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1 5.1 3.5 1.4 0.2 setosa
2 4.9 3.0 1.4 0.2 setosa
3 4.7 3.2 1.3 0.2 setosa
...
51 7.0 3.2 4.7 1.4 versicolor

52 6.4 3.2 4.5 1.5 versicolor
53 6.9 3.1 4.9 1.5 versicolor
...
101 6.3 3.3 6.0 2.5 virginica
102 5.8 2.7 5.1 1.9 virginica
103 7.1 3.0 5.9 2.1 virginica
...

この「iris」というデータは，Iris 属の３種（setosa, versicolor および virginica）の５０標本のそれぞれについて，萼片（sepal）の長さと幅および花弁（petal）の長さと幅という計４項目の計測値が集計されている．ここに示された形態学的な４変量データを例にとって，多変量解析（multivariate analysis）と総称される統計学的ツール群について考えてみよう．

１．〈視覚化〉という戦略：クラスター分析を例にして

基本的な認識として，われわれ人間は多変量が構成する多次元空間の中でのデータ点の特徴をそのまま理解する能力はない．われわれがなんとか理解できるのは，たかだか３次元空間までの低次元のレベルまでである．４次元以上の空間については，それを想像することすら困難を覚える人は少なくない．とすると，多変量解析と称されるツールの基本的な御利益は，そのままでは理解不能な多変量データの特性やパターンを，われわれ人間が理解できるようにしてくれるという点にあると言ってよいだろう．理解不能な対象をなんとか理解できるような形式に仕立て直してくれるという利便を多変量解析の諸手法はわれわれに提供してくれる．もちろん，現在までに開発されている多変量解析の手法は数多くあり，それらを網羅的に扱うことは本章の目指すところではない．むしろ，どのような基本的スタンスに立って多変量データに取り組めばいいのかという理念あるいは姿勢についてここで考えてみたい．
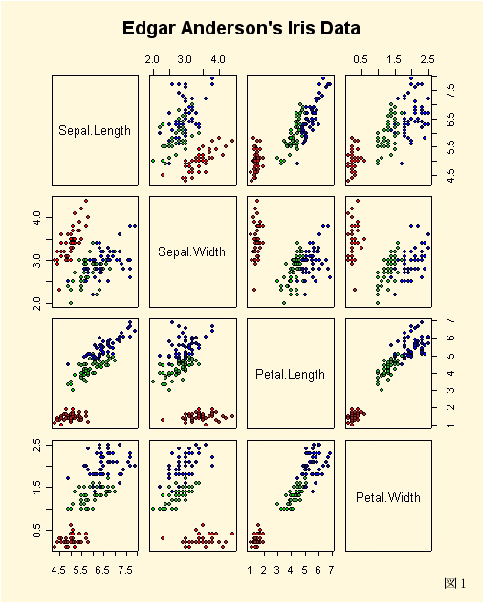
上の「iris」ファイルに代表される多変量データは，数値の羅列をいくら見ていても，そこに含まれているかもしれない特性を見抜くことはほとんど期待できない．こういうときにまずはじめに役に立つのは〈視覚化〉することである．すなわち，グラフや図表を用いることで鳥瞰的に対象を見渡すというスタイルは，多変量データに対してはとくに有効である．たとえば，「iris」に含まれる変量のペアごとに２次元的な散布図を描かせてみよう：

> pairs(iris[1:4], pch = 21, bg = c("red", "green3", "blue")[unclass(iris$Species)])

出力された散布図（図１）を見ると，変量のペアによってはあるパターンの存在が認知されることがわかる．多次元空間の中でこのようなパターンの発見を手助けしてくれるツールが多変量解析である．図１のような変量間の網羅的ペア散布図は，人間にとって相対的に理解しやすい二次元空間の累積として多次元空間内のパターンを知覚させる，［原始的な］多変量解析ツールのひとつだと考えられる．

101 6.3 3.3 6.0 2.5
102 5.8 2.7 5.1 1.9
103 7.1 3.0 5.9 2.1
...

「iris.x」の４変量データから，分類対象間のユークリッド距離を計算し（「dist」コマンド），それを対象間の類似度の尺度とする：

> d.euclid <- dist(iris.x, method="euclid")

次に，群平均法（UPGMA法）によって，クラスターをつくる（「hclust」コマンド）：

> cluster <- hclust(d.euclid, method="average")

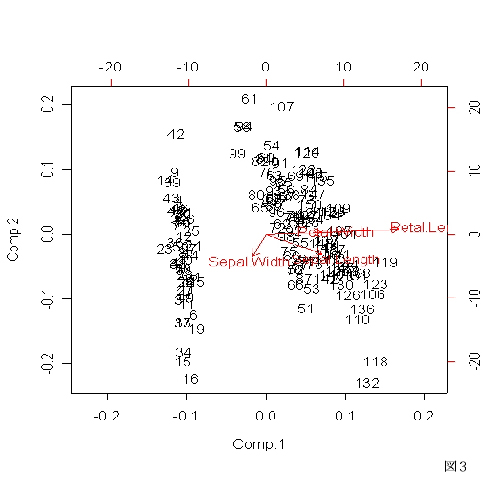
最後に，樹形図を出力する（「plot」コマンド：図２）：

> plot(cluster, hang=-1)

このように，クラスター分析は，多変量データをひとつの実数値（類似度）に変換し，分類対象のグルーピングをグラフ化するという〈視覚化〉を通じて，多変量データの中に潜む類似度の構造を明らかにしようとするツールである．

２．〈次元減少〉という戦略：主成分分析を例にして

〈視覚化〉は確かにひとつの有効な方針である．しかし，多変量解析にとってもうひとつの有用な指針がある．それは〈次元減少〉である．多変量データの理解を阻む大きな要因は，複数の変量が同時的に変動することにある．もしも，何らかの基準のもとで元データの次元（変量数）をうまく減らすことができるならば，人間にとっての理解度はきっと格段に向上するだろう．ここでひとつ注意しておきたい．単に変量の数を減らすだけでは不十分である．削られた変量が重要な情報をもっている可能性はつねにある．さらに言えば，元変量それ自身が別の潜在的要因の部分的発現にほかならないということもあり得る．したがって，多変量データの〈次元減少〉をする際には，次元（変量）を減らす正当な理由がなければならない．
多変量データの〈次元減少〉に主眼を置いた手法のひとつに「主成分分析」（PCA: principal component analysis）と呼ばれる方法がある．多変量空間における主成分（principal component）とは，元変量の線形結合として定義される新しい変量である．第１主成分は多次元空間の中での最大の分散をもつ変量軸であり，元変量の分散共分散行列（あるいは相関係数行列）の最大固有値に対応する固有ベクトルによって決定される．第２主成分は，第１主成分と直行する方向で２番目に大きな分散をもつ変量軸で，２番目に大きな固有値に対応する固有

ベクトルによって決まる．以下，同様にして，軸の直交性を保ちつつ，分散の大きさにしたがって下位の主成分が求められる．
主成分とは，元変量の線形結合を通じて多変量データを要約しようとする．その際の基準は，元の多変量データのもつばらつき（変動）をできるだけ少数の主成分によって説明してしまおうとする姿勢である．もしデータの全変動の大部分がごく少数の主成分によってうまく説明できたならば，多次元空間の低次元空間への〈次元減少〉に成功したことになる．上の「iris」データを用いて，実際に計算してみよう．
あらかじめ「iris」の第５列（種名列）を除いた４変量データファイル「iris.x」について，分散共分散行列に基づく主成分分析を行なう（「princomp」コマンド）：

> pca <- princomp(iris.x)

計算結果を格納したオブジェクト「pca」の中身をチェックする．まずはじめに，各主成分（Comp.1～Comp.4）の分散とその累積和を示す：

> summary(pca)

Importance of components:

Comp.1 Comp.2 Comp.3 Comp.4
Standard deviation 2.0494032 0.49097143 0.27872586 0.153870700
Proportion of Variance 0.9246187 0.05306648 0.01710261 0.005212184
Cumulative Proportion 0.9246187 0.97768521 0.99478782 1.000000000

この結果を見ると，第１と第２のふたつの主成分によって元データの全変動のおよそ９８％が説明されていることがわかる．したがって，このケースでは，元変量の張る４次元空間ではなく，最初のふたつの主成分が張る２次元空間を考えれば十分であることになる．これならば常人でも十分にデータのもつパターンや構造が見通せるだろう．なお，各主成分の分散をグラフ表示することもできる（「plot」コマンド）：

> plot(pca)

続いて，各主成分が元のどの変量と大きく関連しているのかを見てみよう：

> loadings(pca)

Loadings:

Comp.1 Comp.2 Comp.3 Comp.4
Sepal.Length 0.361 -0.657 0.582 0.315

Sepal.Width -0.730 -0.598 -0.320
Petal.Length 0.857 0.173 -0.480
Petal.Width 0.358 -0.546 0.754

それぞれの主成分への元変量の因子負荷量（factor loadings）の絶対値の大きさによって，正または負の関連性の大きさが判定できる．このケースでは，第１主成分は主として花弁の長さ（Petal.Length）から正の大きな影響を受けており，第２主成分は萼片の２形質（Sepal.LengthとSepal.Width）から負の大きな影響を受けている．主成分の生物学的な解釈をする際に，因子負荷量はよい手がかりを与える．
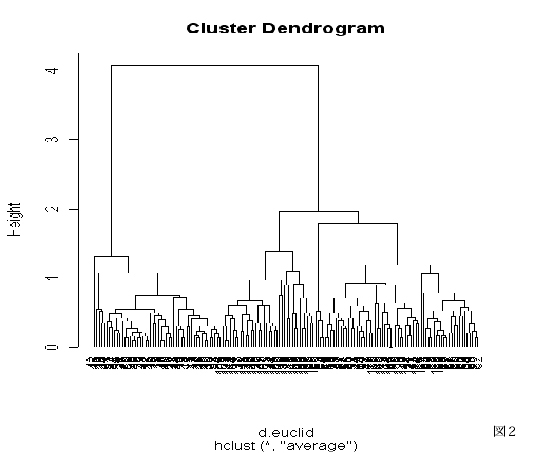
最後に，第１主成分と第２主成分の張る部分空間（平面）での散布図を示そう（「biplot」コマンド：図３）：

> biplot(pca)

元の４次元空間内のデータ点の変動は，主成分分析を通じて，事実上は２次元主成分平面の中で大部分の変動が説明できるということである．

３．〈一般化〉という戦略：多変量分散分析を例にして

１変量から多変量に方法論を〈一般化〉することで，多変量データを解析するツールが提供されるという例もある．とくに，パラメトリック統計学における［一般化］線形モデルは多変量への〈一般化〉が容易である．以下では，単変量分散分析（ANOVA）から多変量分散分析（MANOVA）へという〈一般化〉の戦略を形態測定学を例にとって説明しよう（下の説明は三中 1997, 1999, 2003 による）．
いま２次元平面の中の標識点の集まりによって定義される「かたち」を例に取る．平面上の３標識点Ａ1，Ｂ1，Ｃ1を考える（図４）．いま，この３点Ａ1，Ｂ1，Ｃ1がつくる三角形の底辺を基準線（baseline）に定め，底辺線分Ａ1Ｂ1を数直線上のＡ（位置０）およびＢ（位置１）とする長さ１の線分に変換する．この基準化変換は，変位・回転・スケーリングを組み合わせた変換である．
この変換によって頂点Ｃ1がＣに移動するとき，Ｃをもとの三角形Ａ1Ｂ1Ｃ1の形状座標

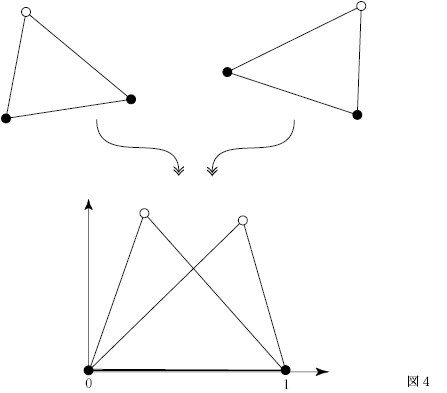
（shape coordinates）と呼ぶ．形状座標の計算式は下記の通りである．３点をＡ1（ｘA，ｙA），Ｂ1（ｘB，ｙB），Ｃ1（ｘC，ｙC）と表わす．このとき，形状座標（ｘshape，ｙshape）は下記のように表される：

ｘshape＝｛（ｘC－ｘA）（ｘB－ｘA）＋（ｙC－ｙA）（ｙB－ｙA）｝／｛（ｘB－ｘA）2＋（ｙB－ｙA）2｝
ｙshape＝｛（ｙC－ｙA）（ｘB－ｘA）－（ｘC－ｘA）（ｙB－ｙA）｝／｛（ｘB－ｘA）2＋（ｙB－ｙA）2｝.

現実世界での生物の「かたち」は，さまざまな変異をもって生じる．かたちの群内・群間変異の検出や差異の検定のための確率的変異モデルとして，円形正規分布モデルを考える．帰無モデルとしての円形正規分布モデルは，２次元平面上の標識点の観測座標値Ｚiが，次の円形正規分布モデルにしたがう確率的変異をすると仮定する：

Ｚi＝Ｗi＋dＺi
Ｚi：観測座標値；
Ｗi：母座標値；
dＺi＝（εix，εiy）：座標値の誤差．
（εix，εiy）～Ｎ（[σ1]2 ０）
（０ [σ2]2）.

各標識点は，ある母座標値の周りで正確な円形の確率円を持つ２次元正規分布に従うと仮定する．

ある三角形の３標識点Ｚi（i=1,2,3）がＺi＝Ｗi＋（εix，εiy）という円形正規分布をするとき，辺Ｚ1Ｚ2のある基準線分（たとえばＷ1Ｗ2）への変換により，この三角形の形状座標は

Ｗ3＋（ν1，ν2）

ただし，ν1とν2はそれぞれεix，εiy（i=1,2,3）の線形結合である；

と近似的に表現できる．εix，εiyは独立かつ同一の正規分布に従うから，上の式は形状座標の誤差変動もまた正規分布によって近似できることを意味している．

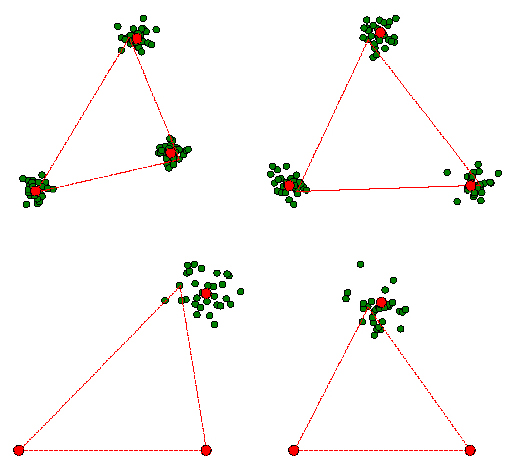
円形正規分布の仮定のもとで，形状座標がある正規分布に近似的に従うことにより，形状座標の差異の有意性検定は標準的な正規分布統計理論のもとで可能になる．たとえば，２つの三角形集団のもとで形状座標の比較をするには，多変量分散分析（MANOVA: multiple analysis of variance: Morrison 1990）を用いればよい．これは，測定値の群内変動(平方和積和行列)に対して群間の差が有意であるかどうかを検定する方法である．たとえば，図５に示す２次元の

仮想例を考えよう（計算は tpsTri によって行なった）．これは，線分ＡＢを規準線として計算された形状座標Ｃから構成される２集団である．この２集団間の座標の平均値の差が有意であることを統計学的に示すことがここでの問題である．この問題は２実変量（２次元座標だから）に対する多変量分散分析によって解決できる．
１変量の分散分析（ANOVA: analysis of variance）の原理を簡単に復習しよう（Morrison 1990: 201-205）．２群について観察された１変量Ｘが下の線形モデルに従うと仮定する：

ｘij＝μ＋αi＋εij　ただし　εij～Ｎ（0,σ^2）
　　　　　　ｘij　第ｉ群の第ｊ番目の観察データ（１変量）
　　　　　　　　　ただし，ｉ＝1,2；ｊ＝1,2,...,ｎi
　　　　　　μ　　μは総平均

　　　　　　αi　第ｉ番目の未知パラメーター（変動因）
　　　　　　εij　正規分布Ｎ（0,σ^2）をする誤差変量．ただし，
　　　　　　　　　誤差は独立かつ同一の分布をすると仮定する．

第ｉ群の標本平均をｍiで，その標本分散をＳiであらわす．このとき，群間に差異がないという帰無仮説「Ｈ0：μ1＝μ2」のもとでの検定統計量Ｆの分布が次のＦ分布である：

Ｆ＝｛（ｎ1＋ｎ2）／ｎ1ｎ2｝・｛（ｍ1－ｍ2）2｝／｛（Ｓ1＋Ｓ2）／
（ｎ1＋ｎ2－２）｝～Ｆ（１, ｎ1＋ｎ2－２）

ことから，Ｆ表を用いた上側検定（５％または１％水準）で群間差の有意性を検定できる．あるいは，Ｆの平方根が自由度ｎ1＋ｎ2－２のｔ分布に従うと考えると，ｔ検定によるまったく同等の検定ができる．

変量の数が増えても，原理は同一である（Morrison 1990: 205-210）．２群１と２に関してｐ個の変量が多変量正規分布をするという仮定のもとでのｎ個（ｎ＝ｎ1＋ｎ2）の観察値の線形モデル：

ｘ＝ＡＭ＋Ｅ
　　　　　　　ｘ：観察値行列（ｎ×ｐ型）
　　　　　　　Ａ：計画行列（ｎ×（ｋ＋１）型）．
　　　　　　　　　ｋはパラメーター（変動因）数．
　　　　　　　Ｍ：パラメーター行列（（ｋ＋１）×ｐ型）
　　　　　　　Ｅ：誤差行列（ｎ×ｐ型）
　　　　　　　　　ただし，誤差は独立かつ同一の
　　　　　　　　　多変量正規分布Ｎ（0,Σ）に従う．
　　　　　　　　　ここに，Σはｐ×ｐ型の分散共分散行列である．

を考える．このとき，群１と２の間の平均値ベクトルｍ1とｍ2との有意差を検定するためには，まず初めに，上のＦ統計量を多変量に一般化したHotellingのＴ^2統計量を計算する：

Ｔ²＝｛ｎ1ｎ2／（ｎ1＋ｎ2）｝Ｄ²

ただし，Ｄ²＝（ｍ1－ｍ2）[t]｛Ａ1＋Ａ2／（ｎ1＋ｎ2－２）｝[-1]（ｍ1－ｍ2）はマハラノビス汎距離（Mahalanobis's generalized distance）の推定値である．（Ｍ[t]は行列Ｍの転置行列を，Ｍ[-1]は逆行列をそれぞれ意味する．）

次に，このHotellingのＴ²統計量の実数倍が次のＦ分布に従う：

Ｆ＝｛（ｎ1＋ｎ2－ｐ－１）／（ｎ1＋ｎ2－２）ｐ｝Ｔ²
～Ｆ（ｐ, ｎ1＋ｎ2－ｐ－１）

ことから，多変量データに対する群間平均値差を検定できる（Rao 1973: 542, 8b.2.14）．

さらに，上のHotellingのＴ²検定は，WilksのΛ検定と関係づけられる（Rao 1973: 542, 8b.2.15）．一般のWilksのΛ統計量とは：

Λ＝｜Ｅ｜／｜Ｈ＋Ｅ｜Ｈ：帰無仮説に対する平方和積和行列
　　　　　　　　Ｅ：誤差に対する平方和積和行列

と定義される．上式で｜・｜は行列式を表わしており，Λの分母と分子はそれぞれ一般化分散（generalized variance）と呼ばれている．ある種の分散比として特徴づけられるこのΛは，２群間の差に関しては，上のHotellingのＴ²統計量によって表現できる（Rao 1973: 542, 8b.2.15）：

Λ＝１／｛１＋Ｔ²／（ｎ1＋ｎ2－２）｝．

したがって，Λ統計量が正確にＦ分布をすることがわかる（Rao 1973: 555, Table 8c.5β）：

｛（ｎ1＋ｎ2－ｐ－１）／ｐ｝×｛（１－Λ）／Λ｝～Ｆ（ｐ, ｎ1＋ｎ2－ｐ－１）．

すなわち，HotellingのＴ²検定はWilksのΛ検定の特別な場合として含まれる．

ｎ個の標識点から得られる形状座標ｎ－２個（基準線の両端点は除く）は，２次元であれば２×（ｎ－２）個の，３次元であれば３×（ｎ－２）個の実変量を持つ．上の多変量分散分析を用いることにより，われわれは形状座標の配置パターン，すなわち標識点によって代表される形状差の群間差を検定できる．
上の「iris」の４変量データに対して，種（“Species”）を変動因とする多変量分散分析を実行してみよう．まずはじめに，４変量を結合して「X」というオブジェクトとして新たに定義する．変動因として“Species”は「factor」コマンドによって因子であることを指定する：

> X <- cbind(Sepal.Length, Sepal.Width, Petal.Length, Petal.Width)
> Species <- factor(Species)

多変量分散分析コマンド「manova」によって，４変量データ「X」を“Species”によって分散分析する：

> iris.manova <- manova(X ~ Species)

出力された結果について，Hotelling T2検定とWilks Λ検定を行なう：

> summary(iris.manova, test="Hotelling-Lawley")

Df Hotelling-Lawley approx F num Df den Df Pr(>F)
Species 2 32.48 580.53 8 286 < 2.2e-16 ***
Residuals 147

> summary(iris.manova, test="Wilks")

Df Wilks approx F num Df den Df Pr(>F)
Species 2 0.023 199.145 8 288 < 2.2e-16 ***
Residuals 147

いずれの検定によっても，種間差は高度に有意であるという結果が得られた．

なお，４変量のそれぞれについての１変量分散分析も実行できる：

> summary.aov(iris.manova)

Response Sepal.Length :

Df Sum Sq Mean Sq F value Pr(>F)
Species 2 63.212 31.606 119.26 < 2.2e-16 ***
Residuals 147 38.956 0.265

Response Sepal.Width :

Df Sum Sq Mean Sq F value Pr(>F)
Species 2 11.3449 5.6725 49.16 < 2.2e-16 ***
Residuals 147 16.9620 0.1154

Response Petal.Length :

Df Sum Sq Mean Sq F value Pr(>F)
Species 2 437.10 218.55 1180.2 < 2.2e-16 ***
Residuals 147 27.22 0.19

Response Petal.Width :

Df Sum Sq Mean Sq F value Pr(>F)
Species 2 80.413 40.207 960 < 2.2e-16 ***
Residuals 147 6.157 0.042

４．おわりに：道を踏みはずすべからず

多変量解析のツールを使おうとするユーザーが陥りがちなのは，知らず知らずのうちにそのツールに使われてしまうという陥穽である．多変量解析の手法を用いたからといって万能薬のようにすべての疑問が解決できるわけではない．ましてや「真実」がその向こうに見えてくるわけでは必ずしもない．クラスター分析に夢を見てしまった1970年代の数量分類学者たちのたどった末路（三中 1997 参照）は，多変量解析ツールのユーザー一般にとって教訓的である．他の統計手法と同じく，多変量解析もまた「推論」のための便法にすぎない．多変量解析のもっとも重要な効用はユーザーにとっての“発見用ツール”あるいは“説得用ツール”となることだと私は理解している．そのためには，ユーザーが自分の取り組もうとしている問題のありかを的確に理解し，その解決のために多変量解析をどのように主体的に使いまわせるのかを考えるという基本的姿勢が必要だろう．しかし，その点を心得違いしてしまったユーザーによって，多変量解析はかぎりなく誤解され得るし，はてしなく誤用され続ける．とても残念なことだ．

参考文献

三中信宏 1997. 『生物系統学』. 東京大学出版会, 東京, xiv+458pp.
三中信宏 1999. 形態測定学. 所収：棚部一成・森啓（編）『古生物の形態と解析』．（朝倉書店, 東京）, pp.61-99.
三中信宏 2003. 生物形態とその変形をどのように定量化するか：幾何学的形態測定学への道. 所収：関村利朗・野地澄晴・森田利仁（編）『生物の形の多様性と進化：遺伝子から生態系まで』（裳華房, 東京），pp.313-328.
Morrison, D.F. 1990. Multivariate Statistical Methods. Third Edition. McGraw-Hill, New York, xx+495pp.
Rao, C.R. 1973. Linear Statistical Inference and Its Applications. Second Edition. John Wiley and Sons, New York, xxii+625pp.［奥野忠一・長田洋・篠崎信雄・広崎昭太・古河陽子・矢島敬二・鷲尾泰俊訳 1977. 『統計的推測とその応用』東京図書, 東京.］
Rohlf, F.J. 2004. tpsTri version 1.19. Computer software for morphometric analysis. Department of Ecology and Evolution, State University of New York at Stony Brook. Available from the internet: <http://life.bio.sunysb.edu/morph/index.html>.