三中信宏
農業環境技術研究所
minaka@affrc.go.jp
http://cse.niaes.affrc.go.jp/minaka/
クラスター分析の基本原理は「似ているものをひとまとめにする」ことにある.ここにはふたつの演算が含まれている.ひとつは,対象物(操作的分類単位:OTU=operational taxonomic unit)間の類似度の数値化である.もうひとつは,計算された類似度にしたがってOTUを群(クラスター)にまとめ上げていくクラスタリングである.以下では,前者について解説する.
数量表形学では,OTU間の類似性を表形的(phenetic)な全体的類似度(overall similarity)によって数値化するという基本的な姿勢がある.その哲学的な動機づけは別として,OTUごとに数値化された形質データがあるとき,OTU間の類似度をどのような尺度によって数値化すればいいのかという問題は,クラスター分析だけではなく,距離法に基づく系統樹推定法の論議にも関わってくる.
対象物間の「似ている程度」は距離(distance)ということばで表現されることがある.しかし,距離という概念の定義と内容を明確にするためには,より厳密な計量性(metricity)の観点から定式化しておく必要があるだろう.x,yを任意のOTUとするとき,ある写像φ(x,y)が計量(metric)であるためには,次の4条件が満足される必要がある:
A1) 非負性(nonnegativity):
φ(x,y)≧0
A2) 対称性(symmetry):
φ(x,y)=φ(y,x)
A3) 確定性(definiteness):
φ(x,y)=0となる必要十分条件はx=yである
A4) 三角不等式(triangle inequality):
φ(x,z)≦φ(x,y)+φ(y,z)
A1とA2は,「距離」のイメージを連想させるので直感的に受け入れられるだろう.A3もまた「同じものならば距離ゼロ」という直感的理解ができる.じっさい,A3で「x=y」とおけば「φ(x,x)=φ(y,y)=0」となる.このA3の代わりに,より緩和された仮定
A3') 擬計量性(pseudometricity):
φ(x,x)=0
を置くと,擬計量(pseudometric)が得られる.このとき,φ(x,y)=0であってもx≠yであることが許される.
三角不等式(A4)が満たされているならば,異なる3点間の「距離」はある三角形の3辺をつくることができる.この条件は,「距離」が‘物理的解釈’できるかどうかという基準を与える.三角不等式を仮定しない距離は非計量(nonmetric)と呼ばれる.
クラスター分析や系統分析では,A4よりもさらに厳しい次の条件群の方がむしろ重要である:
A4') 相加性(additivity):
φ(x,y)+φ(z,u)≦max{φ(x,z)+φ(y,u), φ(x,u)+φ(y,z)}
A4'') 超計量性(ultrametricity):
φ(x,z)≦max{φ(x,y), φ(y,z)}
相加性の条件A4'は,これまで相加的距離(additive distance)の「4点条件(4-point condition)」と呼ばれてきたもの.また,さらに強い超計量性の条件A4''は,1970年代はじめの数量分類学では表形図(phenogram)における距離(ultrametric distance)の満たすべき条件式として登場していた(Jardine & Sibson, 1971, 『Mathematical Taxonomy』 John Wiley & Sons).
以上を要約すると,「距離」が満たすべき条件の組み合わせによって,下記のような定義群が得られる:
A1+A2 pseudometric
A1+A2+A3 nonmetric
A1+A2+A3+A4 metric
A1+A2+A3+A4' additive
A1+A2+A3+A4'' ultrametric
擬計量<非計量<計量の順に定義の厳しさが大きくなっていく.計量性・相加性・超計量性の間にも同じ関係がある:
【命題1】超計量性は相加性を含意し,相加性は計量性を含意する.逆は成立しない.
【証明】1)超計量性→相加性の証明:任意のx,y,zに対して超計量性「A4''」が成立するとき,φ(x,z)≦max{φ(x,y), φ(y,z)}.一方,相加性「A4'」の条件式でz=uであるとき:
φ(x,y)+φ(z,z)≦max{φ(x,z)+φ(y,z), φ(x,z)+φ(y,z)}
左辺第2項はゼロ,右辺は同一の項になるので:
φ(x,y)≦φ(x,z)+φ(y,z) (i)
「A4''」と(i)の左辺どうしを比較すればよい.□
2)相加性→計量性の証明:上の(i)は三角不等式「A4」と一致するので,自明.□
三角不等式「A4」は三角形の3辺をなすという幾何学的解釈が可能だ.相加性と超計量性についても同様の解釈ができる.それを示すために,次の【命題2】をまず提示する:
【命題2】3実数X,Y,Z(X≦Y≦Z)の間に X≦max{Y,Z};Y≦max{Z,X};Z≦max{X,Y} が成り立つとき,X≦Y=Z.
【証明】3数の大小関係により,
X≦max{Y,Z}=Z (1)
Y≦max{Z,X}=Z (2)
Z≦max{X,Y}=Y (3)
前提により(1)は成立.(2)と(3)から Y=Z が導かれる.よって,X≦Y=Z.□
この結果を利用して,次の命題が証明できる:
【命題3】
1)x,y,zに関してφ(x,y),φ(x,z),φ(y,z)が超計量性を満たすとき,最大の二つは互いに等しく,残る一つよりも大きい.
2)x,y,z,uに関してφ(x,y),φ(x,z),φ(y,z),φ(y,z),φ(y,u),φ(z,u)が相加性を満たすとき,三つの和φ(x,y)+φ(z,u),φ(x,z)+φ(y,u),φ(x,u)+φ(y,z)のうち,最大の二つは互いに等しく,残る一つよりも大きい.
【証明】1)一般性を失うことなくφ(x,y)≦φ(x,z)≦φ(y,z)と仮定できるので,X=φ(x,y),Y=φ(x,z),Z=φ(y,z)と置くことにより,命題2が適用される.□
2)一般性を失うことなくφ(x,y)+φ(z,u)≦φ(x,z)+φ(y,u)≦φ(x,u)+φ(y,z)と仮定できるので,それぞれの和をX,Y,Zと置くことにより,命題2が適用される.□
この【命題3】は,超計量性あるいは相加性を満足する計量が,ある計量空間の中で「等辺が底辺よりも長い二等辺三角形」を形成することを意味している.超計量の場合は,三角不等式をより強く制約したかたちで,同じ空間内で二等辺三角形を形成する.一方,相加性を満たす計量の場合は,それが二等辺三角形をつくる別の計量空間を導出する必要がある.Semple & Steel の『Phylogenetics』の第7章では次の命題が示されている:
【命題4】(Semple & Steel 2003: 149, Lemma 7.2.2)
OTU集合X上の計量δが相加性を満足するのは,Xの任意の点rに対するGromov積δ[r]=(1/2){δ(x,y)−δ(r,x)−δ(r,y)}が超計量であるときそしてそのときに限られる.
【証明】
1)δ[r]の超計量性→δの相加性の証明:
超計量性条件「A4''」により:
δ[r](x,z)≦max{δ[r](x,y),δ[r](y,z)}
Gromov積の定義により:
(1/2)[δ(x,z)−δ(x,r)−δ(z,r)]≦
max{(1/2)[δ(x,y)−δ(x,r)−δ(y,r)],(1/2)[δ(y,z)−δ(y,r)−δ(z,r)]}
両辺を2倍して,δ(x,r)+δ(y,r)+δ(z,r)を加えると:
δ(x,z)+δ(y,r)≦max{δ(x,y)+δ(z,r),δ(x,r)+δ(y,z)}
これは相加性条件「A4'」にほかならない.□
2)δの相加性→δ[r]の超計量性の証明:
上の式変形を逆にたどれば自明.□
上で導入された「Gromov積」とは,分岐分析(Wagner樹計算)の過程で,ある枝と点との距離の計算式(Semple & Steelは「Farris変換」と名づける)として登場するものと同一の絶対値をもつ.
クラスター分析のデンドログラムと超計量とは完全に対応付けられる.いま,デンドログラムの根ρからOTU集合にいたる祖先子孫関係の半順序(partial order)≦を考える.デンドログラムの枝に対して
i)任意のOTUのペアx,yに対して<その直接共有祖先ρからのδは互いに等しい:δ(ρ,x)=δ(ρ,y).
ii)あるxと内点(仮想的分類単位:HTU=hypothetical taxonomic unit)uとvの間にu≦v≦xなる関係があるとき,δ(x,v)≦δ(x,u)となる
という条件を満たす重み(枝長)を対応付ける関数を「等距離重み付け(equidistant weighting)」と定義する.いまx,y,zに対してx,yの直接共通祖先vとx,y,zの直接共通祖先uとの間にはu≦vなる関係があるので,iによりδ(x,y)≦δ(x,z)かつδ(x,y)≦δ(y,z),iiによりδ(x,z)=δ(y,z).よって,【命題3】によりδは超計量となる.その逆も成立し,次の命題が証明できる.
【命題5】(Semple & Steel 2003: 151, Theorem 7.2.5)
計量δが超計量であるための必要十分条件は,δの等距離重み付けが存在することである.
この命題により,超計量を図示するクラスター分析のデンドログラムは,ある分岐点から派生するすべての末端OTUへの長さが等距離であるという性質をもつ.言い換えれば,超計量は上の意味で「等距離」表示ができるということ.
一方,相加性をもつ計量と樹形図との間にも同様の関係がある.
【命題6】(Semple & Steel 2003: 152, Theorem 7.2.6「Tree-Metric Theorem」)
計量δが相加的であるための必要十分条件は,樹形図(tree)として表示できることである.
デンドログラムは,相加的計量をいつも正確に表現できるわけではない.相加的計量を正確に表現するためには,相加的樹形図(additive tree)というグラフが必要になるが,これは超計量的樹形図(ultrametric tree)よりも枝長に関して制約の緩いグラフである.なぜなら,相加的樹形図はある分岐点から末端OTUまでの距離が互いに異なることを許容するからである.
さらにいえば,クラスター分析のデンドログラムは「特殊な超計量的樹形図」であり,クラスターの分岐点の「高さ」がOTU間の距離(超計量値)それ自身を示していて,等距離重み付けから得られる超計量的樹形図とは樹形が同じでも枝長は異なる.その理由は,デンドログラムでは分岐点の高さ(クラスター・レベル)によって距離を表現するのに対し,超計量樹ではグラフの辺(edge)の長さ(の和)によって距離を表現するというちがいがあるからである.Semple & Steel (2003: 150)のことばを借りれば,超計量的樹形図は枝(辺)に超計量値を付与した「等距離表現(equidistant representation)」であるのに対し,デンドログラムは内点に超計量値を付与した「頂点表現(vertex representation)」をしていると言うことができる.両者は正確に対応しているのだが(isomorphicということ),樹形図の解釈をするときに混乱するおそれはあるだろう.
超計量性や相加性など計量のもつ条件を実際のデータが満足しているとはかぎらない.また,表現手段としての樹形図が計量のもつ性質を正確に表示できるともかぎらない.たとえば,データが真に超計量的であったとしたら,デンドログラムやそれと同型の超計量的樹形図は完全に正確にそのデータを表示できるだろう.しかし,データが相加的であっても超計量的ではなかったとしたら,そのデータから導かれたデンドログラムは正確な表示をしていないことになる.すなわち,デンドログラムから導出される常に超計量としてのOTU間の距離尺度と元のデータに示される距離尺度との相関関係(共表形相関係数cophenetic correlation coefficient)は,データと樹形図との対応が悪くなるとともに値が低下する.
実際のクラスター分析で用いられる計量の定義式にはさまざまなものがある.生物学で最もよく用いられているのは「ミンコフスキー計量(Minkowski metric)」というカテゴリーに属する距離尺度である:
ミンコフスキー計量(Minkowski metric)
D(x,y)={Σ[k=1〜p](w[k]・|x(k)−y(k)|^λ)}^(1/λ)
x,y:OTU
x(k),y(k):第k形質値(k=1,2,...,p)
w[k]:第k形質の重み
λ:累乗パラメータ
パラメータλを変化させることにより,次の二つの計量が導出される(いずれもw[k]=1とする):
λ=1→マンハッタン計量(Manhattan metric)
Dm(x,y)=Σ[k=1〜p](|x(k)−y(k)|
λ=2→ユークリッド計量(Euclidean metric)
De(x,y)={Σ[k=1〜p](|x(k)−y(k)|^2)}^(1/2)
いずれも,数量分類学および系統推定論ではもっとも広く使われる計量である.
以下,〈R〉を用いた簡単な実例を通して説明する.
●距離行列を入力データとして「agnes」でクラスタリング
○超計量距離データ
> library(cluster) # ライブラリー「cluster」のオープン
> test.d <- c(2,6,10,6,10,10)
# 距離行列の成分をキー入力し,オブジェクト「test.d」に格納する.
OTU1〜4間の下記の距離値を列ごとにベクトルとして入力した:
OTU1 OTU2 OTU3
OTU1
OTU2 2
OTU3 6 6
OTU4 10 10 10
> test.d
[1] 2 6 10 6 10 10
# 入力データの確認
> agn <- agnes(test.d, diss = TRUE, method = "average")
# agnesに「test.d」を距離行列として入力し,群平均法でクラスタリングする.
> plot.agnes(agn, which.plots=2, hang=-1)
# 結果のデンドログラム表示
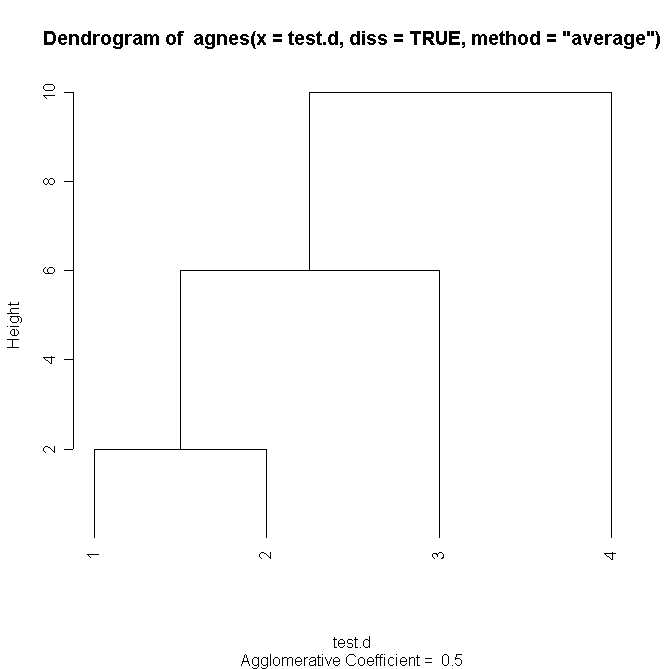
「agnes」を使えば,形質データ行列ではなく,ユーザーが自分で計算した距離行列からもクラスタリングできる.
なお,もともとのデータが超計量的であるとき,上のデンドログラムから導かれるOTU間の距離行列は元の距離行列と完全に一致する(すべての行列成分が同一だから).したがって,共表形相関係数の値は1となる.
デンドログラムは超計量の「頂点表示」図式だが,同型で「等距離表示」を可能にする超計量的樹形図を描くことはたやすい.この場合,枝長の和が長距離となるようにする.
3.5 0.5 1
━━┳━━┳━━┳━━ 1
┃ ┃ ┃1
┃ ┃ ┗━━ 2
┃ ┃ 1.5
┃ ┗━━━━━ 3
┃ 5
┗━━━━━━━━ 4
━━┳━━┳━━┳━━ 1
┃ ┃ ┃1
┃ ┃ ┗━━ 2
┃ ┃ 1.5
┃ ┗━━━━━ 3
┃ 5
┗━━━━━━━━ 4
○相加的距離データ
> library(cluster)
# ライブラリー「cluster」をオープン.
> test.d <- c(6,7,14,3,10,9)
# 相加的距離データをキー入力
OTU1〜4間の下記の距離値を列ごとにベクトルとして入力した:
OTU1 OTU2 OTU3
OTU1
OTU2 6
OTU3 7 3
OTU4 14 10 9
> test.d
# 入力した距離行列「test.d」の確認
[1] 6 7 14 3 10 9
> agn <- agnes(test.d, diss = TRUE, method = "average")
# 群平均法でクラスタリングして,結果をagnes.object「agn」に格納.
> plot.agnes(agn, which.plots=2, hang=-1)
# デンドログラムの描画

> cutree(agn, c(1,2,3,4))
# ルートからのクラスター構成を表示.
1 2 3 4
[1,] 1 1 1 1
[2,] 1 1 2 2
[3,] 1 1 2 3
[4,] 1 2 3 4
> agn
# agnes.object「agn」の中身の表示.
Call: agnes(x = test.d, diss = TRUE, method = "average")
Agglomerative coefficient: 0.4659091
Order of objects:
[1] 1 2 3 4
Height (summary):
Min. 1st Qu. Median Mean 3rd Qu. Max.
3.000 4.750 6.500 6.833 8.750 11.000
Available components:
[1] "order" "height" "ac" "merge" "diss" "call" "method"
以下は,オブジェクト「agn」の内容をひとつひとつ表示させた.
> agn$height
# クラスターがリンクする距離(超計量)
[1] 6.5 3.0 11.0
> agn$ac
# 凝集係数(agglomerative coefficient)
[1] 0.4659091
> agn$merge
[,1] [,2]
[1,] -2 -3
[2,] -1 1
[3,] 2 -4
> agn$diss
# 距離データの表示
Dissimilarities :
[1] 6 7 14 3 10 9
Metric : unspecified
Number of objects : 4
上のデンドログラムは,超計量ではないが,相加的ではあるデータの場合,デンドログラムから得られた超計量距離行列(6.500, 6.500, 11.000, 3.000, 11.000, 11.000)と元の距離行列(6, 7, 14, 3, 10, 9)との間にちがいがあることを示している.このときの共表形相関係数は〈R〉を用いて,下記のように計算できる:
> original.data <- c(6, 7, 14, 3, 10, 9) # 元の距離行列
> dendrogram.data <- c(6.500, 6.500, 11.000, 3.000, 11.000, 11.000)
# デンドログラムからの超計量距離行列
> cpcc <- cor(original.data, dendrogram.data)
# 共表形相関係数の計算
> cpcc # 共表形相関係数の表示
[1] 0.8917926
相加的計量は相加的樹形図を用いれば正確にその距離情報を表現することができる.
w x
┏━━┳━━┳━━ 1
┃ ┃ ┃y
┃ ┃ ┗━━ 2
┃ ┃ z
┃ ┗━━━━━ 3
┃ u
┗━━━━━━━━ 4
┏━━┳━━┳━━ 1
┃ ┃ ┃y
┃ ┃ ┗━━ 2
┃ ┃ z
┃ ┗━━━━━ 3
┃ u
┗━━━━━━━━ 4
相加的樹形図の各枝の枝長を未知数とおくと,OTU間の距離から,連立方程式を立てることができる:
d(1,2)=x+y=6
d(1,3)=x+w+z=7
d(1,4)=x+w+u=14
d(2,3)=y+w+z=3
d(2,4)=y+w+u=10
d(3,4)=z+u=9
d(1,4)−d(2,4)=x−y=4とd(1,2)=x+y=6より,x=5,y=1.d(1,4)−d(1,3)=u−z=7とd(3,4)=u+z=9より,u=8,z=1となる.結果は下記の通り:
1 5
┏━━┳━━┳━━ 1
┃ ┃ ┃1
┃ ┃ ┗━━ 2
┃ ┃ 1
┃ ┗━━━━━ 3
┃ 8
┗━━━━━━━━ 4
┏━━┳━━┳━━ 1
┃ ┃ ┃1
┃ ┃ ┗━━ 2
┃ ┃ 1
┃ ┗━━━━━ 3
┃ 8
┗━━━━━━━━ 4
相加性をもつ距離情報が正確に表現されていることがわかる.
参考文献
【書名】Mathematical Taxonomy
【著者】Nicholas Jardine and Robin Sibson
【刊行】1971
【出版】John Wiley & Sons, London
【叢書】Wiley Series in Probability and Mathematical Statistics
【頁数】xviii+286 pp.
【ISBN】0-471-44050-7
【書名】Phylogenetics
【著者】Charles Semple and Mike Steel
【刊行】6 February 2003
【出版】Oxford University Press, Oxford
【叢書】Oxford Lecture Series in Mathematics and Its Applications 24
【頁数】xiv+239 pp.
【定価】£45.00 (hardcover)
【ISBN】0-19-850942-1
(8 September 2003)