二変量正規分布の2D/3Dグラフィクス
三中信宏
Copyright (c) 2007 by MINAKA Nobuhiro. All rights reserved.
多変量同時確率分布を描画することにより,各変量それぞれの変動(variation)だけでなく,変量間の共変動(covariation)についての直感的な理解を深まるだろう.以下では,〈R〉の多変量正規分布パッケージ〈mvtnorm〉と三次元描画パッケージ〈scatterplot3d〉:
mvtnorm: Multivariate Normal and T Distribution (version 0.8-1)
scatterplot3d: 3D Scatter Plot (version 0.3-25)
を用いて,二変量正規分布の点の散布パターンと密度関数の描画を行なう〈R〉スクリプトを書いた.
1. 基本事項
p次元の変量ベクトル x を考える:
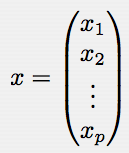
x の同時確率密度関数 f(x) は下記の通りである:
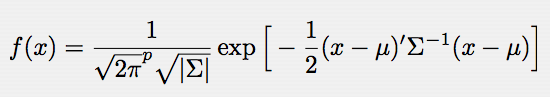
この式の平均ベクトルμと分散共分散行列Σはそれぞれ次式で定義される:
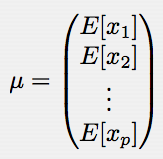
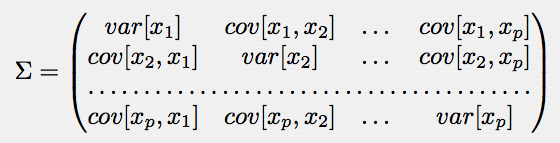
分散共分散行列の各要素(すなわち分散と共分散)は,任意の変量の対に関する偏差積の期待値として定義される:
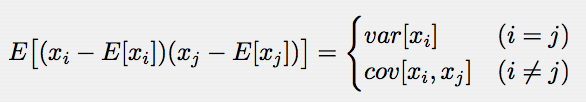
分散共分散行列は,正定値(positive definite)な対称行列であるから,多変量正規分布の密度関数の指数部分に現れる二次形式は,p次元の“楕円”を表わす.したがって,そのグラフを等確率面で切断すれば「等確率楕円」となる.
以下では,p=2 の二変量正規分布を例にとって説明する.まずはじめに,乱数を抽出することにより,点の散布パターン(2D/3D)を確認したのち,密度関数のグラフを示す.
2. 変量間に相関がない場合の散布パターン
R を起動して,インストール済みの〈mvtnorm〉と〈scatterplot3d〉を呼び出す:
> library(mvtnorm) #〈mvtnorm〉の呼び出し > library(scatterplot3d) #〈scatterplot3d〉の呼び出し
変量間に相関がないとき,分散共分散行列の非対角要素はすべてゼロになる.ここでは,各変量の分散が1であるとする.このとき,二変量正規分布の分散共分散行列は単位行列と指定できる:
> sigma.zero <- matrix(c(1,0,0,1), ncol=2) #単位行列を分散共分散行列 sigma.zero と定義する
> sigma.zero
[,1] [,2]
[1,] 1 0
[2,] 0 1
rmvnorm二変量正規分布から抽出する乱数の個数を変化させて,対応する二次元散布図と三次元確率密度関数を描画する.まずはじめに,乱数の抽出個数を 100, 1000, 10000 と変化させて,得られた乱数をそれぞれ別のオブジェクトに格納する:
> x100 <- rmvnorm(n=100, mean=c(0,0), sigma=sigma.zero) #抽出個数100個 > x1000 <- rmvnorm(n=1000, mean=c(0,0), sigma=sigma.zero) #抽出個数1000個 > x10000 <- rmvnorm(n=10000, mean=c(0,0), sigma=sigma.zero) #抽出個数10000個
この正規乱数セットに対する二次元散布図を plot() を用いて描く:
> plot(x100) #左図 > plot(x1000) #中図 > plot(x10000) #右図
さらに,対応する三次元散布図は scatterplot3d() を用いて描く:
> scatterplot3d(x100[,1], x100[,2], dmvnorm(x100, mean=c(0,0), sigma=sigma.zero), + highlight=TRUE) > scatterplot3d(x1000[,1], x1000[,2], dmvnorm(x1000, mean=c(0,0), sigma=sigma.zero), + highlight=TRUE) > scatterplot3d(x10000[,1], x10000[,2], dmvnorm(x10000, mean=c(0,0), sigma=sigma.zero), + highlight=TRUE)
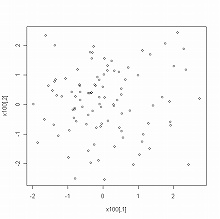
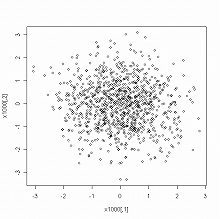
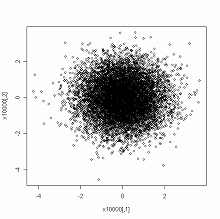
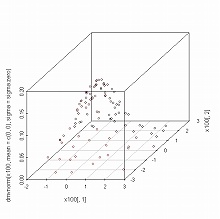
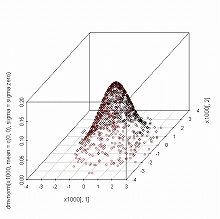
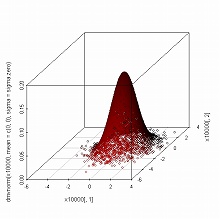
scatterplot3d() を用いたグラフでは,縦軸が確率密度を表わしている.
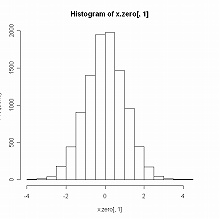
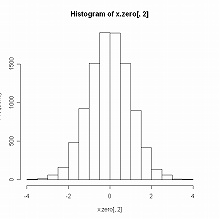
なお,多変量正規分布の同時分布(joint distribution)から得られた周辺分布(marginal distribution)もまた正規分布であることは,そのヒストグラムを hist() で描けばよくわかる:
> x.zero <- rmvnorm(n=10000, mean=c(0,0), sigma=sigma.zero) #正規乱数10000個 > hist(x.zero[,1]) #第一変量の周辺分布ヒストグラム(左図) > hist(x.zero[,2]) #第二変量の周辺分布ヒストグラム(右図)
3. 変量間に相関がある場合の散布パターン
変量間に正または負の共分散がある場合を考える.このとき,分散共分散行列はそれぞれ次のように定義する:
> sigma.positive <- matrix(c(1,0.6,0.6,1), ncol=2) #共分散を「+0.6」に設定した
> sigma.positive
[,1] [,2]
[1,] 1.0 0.6
[2,] 0.6 1.0
> sigma.negative <- matrix(c(1,-0.6,-0.6,1), ncol=2) #共分散を「−0.6」に設定した
> sigma.negative
[,1] [,2]
[1,] 1.0 -0.6
[2,] -0.6 1.0
この設定のもとで,それぞれの二変量正規分布から10000個の乱数を発生させ,2D/3Dの散布図を描いた:
> x.positive <- rmvnorm(n=10000, mean=c(0,0), sigma=sigma.positive) > plot(x.positive) #正の共分散があるとき(左図) > scatterplot3d(x.positive[,1], x.positive[,2], dmvnorm(x.positive, mean=c(0,0), + sigma=sigma.positive), highlight=TRUE) > x.negative <- rmvnorm(n=10000, mean=c(0,0), sigma=sigma.negative) > plot(x.negative) #負の共分散があるとき(右図) > scatterplot3d(x.negative[,1], x.negative[,2], dmvnorm(x.negative, mean=c(0,0), + sigma=sigma.negative), highlight=TRUE)
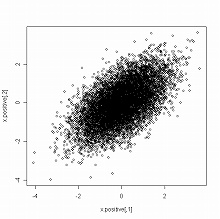
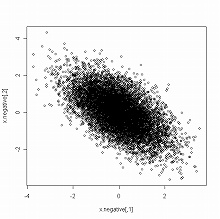

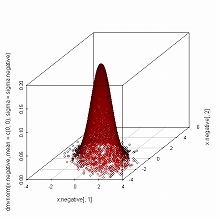
共分散の正負にしたがって,二変量正規分布の密度関数のグラフを等密度平面で切ったときの等確率楕円の軸の方向が変化していることに注意されたい.
4. 二変量正規分布の密度関数のグラフ
上では,二変量正規分布からの乱数抽出を手がかりにして,点の散布パターンを実際に見てきた.以下では,解析的に書かれた密度関数の数式のグラフを三次元表示関数 persp を用いて描いてみる.最初に関数の定義域を入力する:
> x1 <- seq(-3, 3, length=50) # -3≦x1≦3 の範囲を考える. > x2 <- x1 # -3≦x2≦3 の範囲を考える.
変量間の共分散がゼロである場合は下記の通り:
> f <- function(x1,x2) { dmvnorm(matrix(c(x1,x2), ncol=2), mean=c(0,0), sigma=sigma.zero) }
# 上の sigma.zero を分散共分散行列とする密度関数
> z <- outer(x1, x2, f) # X1とX2の定義域の外積に対するfの値域
> z[is.na(z)] <- 1 # z に関する条件
> op <- par(bg = "white") #グラフィクスの環境設定
> persp(x1, x2, z, theta = 30, phi = 30, expand = 0.5, col = "lightblue")
#共分散がゼロである場合の3Dグラフィクス描画
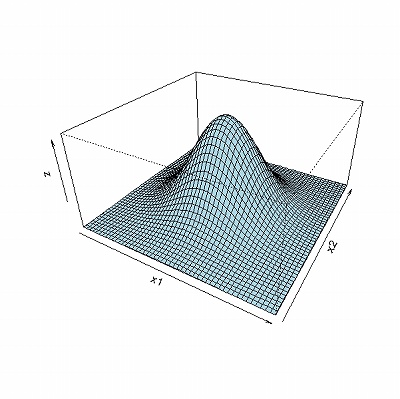
同様にして,共分散が正・負それぞれの場合の密度関数のグラフを下記に示す:
> f <- function(x1,x2) { dmvnorm(matrix(c(x1,x2), ncol=2), mean=c(0,0), sigma=sigma.positive) }
# 上の sigma.positive を分散共分散行列とする密度関数
> z <- outer(x1, x2, f)
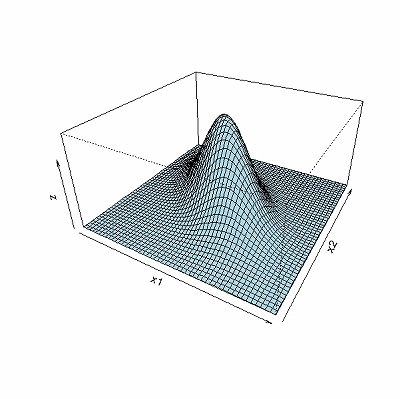
> persp(x1, x2, z, theta = 30, phi = 30, expand = 0.5, col = "lightblue")
#共分散が正である場合の3Dグラフィクス描画

> f <- function(x1,x2) { dmvnorm(matrix(c(x1,x2), ncol=2), mean=c(0,0), sigma=sigma.negative) }
# 上の sigma.negative を分散共分散行列とする密度関数
> z <- outer(x1, x2, f)
> persp(x1, x2, z, theta = 30, phi = 30, expand = 0.5, col = "lightblue")
#共分散が負である場合の3Dグラフィクス描画
5. 参考文献
- B. エヴェリット著(石田基広・石田和枝・掛井秀一訳)『RとS-PLUSによる多変量解析』(2007年6月28日刊行, シュプリンガー・ジャパン, ISBN:978-4-431-71312-8 → 目次)
- 竹村彰通『統計[第2版]』(2007年9月25日刊行, 共立出版[共立講座・21世紀の数学:第14巻], ISBN:978-4-320-01851-8 → 目次|コンパニオン・サイト)